Сдвиги колец Френеля относительно растра изображения

Информация о материале
Категория: Испытательное изображение - кольца Френеля
Опубликовано: 13.02.2019 19:58
Автор: Павел Варгин

Вводя эти параметры, например, в выражение (15), различая горизонтальный и вертикальный размеры сенселя: Δx и Δy, определяя постоянную составляющую – F0 и амплитуду – F1 синусоидального профиля, получим следующее выражение для элемента изображения колец Френеля:

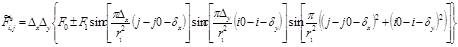.(25)

Обратим внимание на то, что параметры вводятся со знаком минус в выражения для координат по осям x и y в соответствии с индексами параметров. При этом положительные значения самих параметров соответствуют сдвигу изображения колец вправо по оси x и вверх по оси y относительно системы координат x, y и привязанной к ней системы координат j, i. Отрицательные значения параметров соответствуют сдвигу изображения колец в противоположных направлениях.

Поскольку мы произвольно выбираем (задаем) сенсель 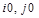, в зону которого попадает центр колец Френеля, следует ограничить области задания параметров  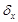и 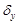, так чтобы при их введении центр колец не покидал зону заданного сенселя. Для неперекрывающихся сенселей значения параметров сдвига не превышают половины максимально возможных размеров сенселя (расстояний между сенселями) по горизонтали или вертикали, то есть: , .

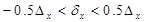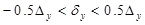При сдвиге изображения колец изменяется радиус колец посторонних узоров (ПУ). На рис. 9 приведен набор из 12 картин колец ПУ первого порядка, при последовательном сдвиге колец Френеля с интервалом –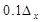 , при 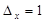. Радиусы полосатых колец ПУ соответствуют узким границам между кольцами, которые представляют собой зоны минимального контраста (различия) между сигналами соседних сенселей фотодатчика. Между этими границами контраст полосок колец ПУ нечетных порядков возрастает. Радиус кольца ПУ определяется выражением:

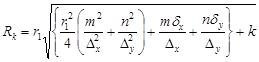,                   (26)

где: фигурными скобками обозначена дробная часть числа 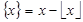,  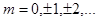– порядок ПУ по оси x,  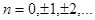– порядок ПУ по оси y, 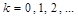– номер кольца. Положение центра кольца ПУ, заданное координатами Xm и Yn определяется выражениями:

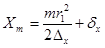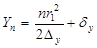,           .                      (27)

Вариант вывода выражений (26) и (27) для одномерной дискретизации приведен в работе [3] с использованием собственных обозначений.

С помощью выражений (27) можно выбирать положение центра подматрицы матрицы изображения колец Френеля, на которой отображается небольшая часть изображения, включающая зону ПУ, как это сделано для фрагментов рис. 9. Непосредственному наблюдению колец ПУ высших нечетных порядков мешает снижение контраста изображения соседних (полосатых) колец из-за ослабляющего действия sinc – функций выражения (25). Кольца ПУ четных порядков, не имеющие полосатой структуры, испытывают инверсию и также теряют межкольцевой контраст с увеличение их порядка. Можно искусственно повысить контраст участка (подматрицы) изображения колец Френеля, содержащего зону ПУ заданного порядка. На рис. 10, полученном с использованием выражения (25), проведено местное контрастирование ПУ четвертого порядка (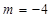) по горизонтальной оси и второго (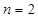) по вертикальной в условиях когда 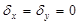. При этом хорошо видны последствия четырехкратной инверсии яркости колец ПУ в районе нулей sinc – функций выражения (25). При математическом моделировании для устранения снижения контраста колец ПУ достаточно исключить в выражении (25) sinc – функции, тем самым переходя, по существу, к выражениям типа (9) или (10). Для случая использования изображения фотодатчика такая операция включает деление функции модуляции яркости этого изображения на соответствующие sinc – функции, что осложняется необходимостью деления на ноль.

В цифровой системе передачи изображений могут использоваться различные сетки растра изображения. Как правило, это прямоугольные периодические структуры, хотя могут быть представлены и треугольные или шестиугольные (гексагональные) сетки. Подход к анализу таких структур, при воспроизведении колец Френеля, аналогичен подходу, использованному при анализе выражения (22).  

Особый интерес вызывает применение колец Френеля для испытаний систем передачи цветного изображения. В таких системах осуществляется цветоделение исходного оптического изображения. В случаях последовательного цветоделения, а также параллельного цветоделения с помощью полупрозрачных зеркал или призм формируются одноцветные компоненты с кольцами Френеля, анализ которых ничем не отличается от вышеизложенного. В современных видеосистемах наиболее распространенным является метод пространственного цветоделения с использованием больших массивов цветных светофильтров. В качестве примера, на рис. 11 а приведены фрагменты различных массивов цветных светофильтров, осуществляющих пространственное цветоделение изображения. При моделировании воспроизводства черно-белых колец Френеля в таких системах передачи, следует учитывать ряд особенностей одноцветных компонент. В одном случае, например, при использовании фильтра Байера, каждая одноцветная (красная, зеленая или синяя) компонента

 формируется из сигналов массива сенселей находящихся под светофильтрами данного цвета путем интерполяции значений сигналов этих сенселей в местах соответствующих положениям сенселей других  цветовых компонент. Массивы сенселей различных компонент отличаются здесь друг от друга сдвигом, кратным межсенсельному расстоянию фотодатчика относительно центра колец Френеля. В других случаях компоненты могут отличаться также периодами своих сеток, комбинациями периодов и содержанием сигналов соответствующего цвета в сигналах сенселей со светофильтрами комбинированных (неосновных) цветов.

Во всех случаях при модельном синтезе цветного изображения колец Френеля следует для любого заданного массива цветных светофильтров (рис. 11 а) определить сетки (матрицы) фильтров одного цвета с индексом – Col с элементами –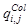 , такими, что 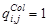, если светофильтр сенселя соответствует указанному цвету и 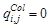, если нет. Затем определить сигналы исходных изображений одноцветных компонент в соответствии с выражением:

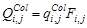,               (28)

где 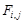 – элемент черно-белого изображения колец Френеля, индексы которого i и j соответствуют выражению (9).

Существуют различные алгоритмы интерполяции значений цветовой компоненты в местах сенселей со светофильтрами другого цвета [4].

Определим  сигналы изображений компонент основных цветов, в случае линейной интерполяции, для массивов основных цветов: Байера и X-Trans Fuji (рис.11 а) в соответствии с выражением:

Если 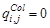 , то ,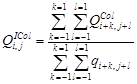                    

если нет, то 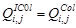.                                            (29)

При такой интерполяции следует ввести граничные условия, например:

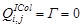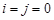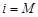, если: , или , или 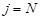.            (30)

В выражении (29) для интерполяции используется подматрица размером 3 х 3. В соответствии с рис. 11 а, здесь для индекса – Col возможны следующие значения, выделенные жирным шрифтом: красный (Red), синий (Blue), зеленый (Green).

Синтезируем, например, цветное изображение колец Френеля с использованием массива фильтра Байера. Введем функцию – указатель кратности двух чисел а и b:

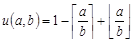,               (32)

где:  – обозначение Айверсона функции – «потолок» – округление вверх, при этом 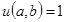 если a делится на b без остатка и  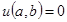если нет.

Сетки для красной (red), синей (blue) и зеленой (green) компонент цветного изображения задаются соответствующими выражениями:

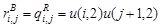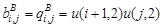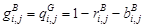,        , ,                                         (33)

а сигналы исходных изображений одноцветных компонент: красной – 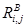, зеленой –  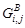и синей –  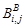изображения колец Френеля, например, с синусоидальным профилем, задаваемым выражением (25), определяются в соответствии с выражениями:

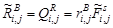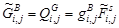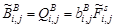,     ,     .     (34)

Сигналы интерполированных изображений одноцветных компонент:

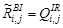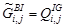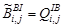,         ,      ,                   (35)

определяются в соответствии с выражением (29).

На рисунке 11 приведены цифровые изображения колец Френеля с прямоугольным (бинарным) радиальным профилем и усреднением по площади сенселя: черно-белого фотодатчика – (б); с фильтром Байера без интерполяции – (в); с X-Transфильтром без интерполяции – (г); Байера с интерполяцией и сдвигом влево на половину сенселя – (д); Байера без сдвига – (е); Байера со сдвигом вправо –(ж)  ; с X-Trans с интерполяцией и сдвигом влево – (з); с X-Trans без сдвига – (и); с X-Trans со сдвигом вправо – (к). Везде хорошо видны посторонние узоры, связанные с дискретизацией изображения колец.

Обратим внимание на то, что посторонние узоры характерны для каждого типа датчика изображения и изменяются при сдвиге положения колец Френеля относительно растра датчика.

Описанные в статье математические модели дискретизации испытательных изображений в виде колец Френеля позволяют рассчитать идеальные картины воспроизводства колец с помощью различных датчиков изображений. Такие картины необходимы при разработке методик и средств измерений для оценки качества систем передачи и обработки изображений. Использование колец Френеля или их частей для этих целей оправдано тем, что методы измерений передаточных характеристик систем передачи и обработки изображений, в этом случае, являются прямыми и, следовательно, потенциально наиболее точными.

Ранее статья опубликована в [5].