Струна
- Информация о материале
- Категория: Математическая модель улитки внутреннего уха
- Опубликовано: 10.01.2015 11:48
- Автор: Павел Варгин
Будем представлять основную мембрану улитки, как совокупность натянутых струн, подобно ряду струн фортепьяно или арфы. В отличие от музыкальных инструментов, здесь струны соединены общей перепонкой, которая весьма слабо связывает струны между собой, но добавляет сопротивления их колебаниям со стороны жидкостей промежуточного и обратного каналов улитки, в которых они колеблются. Эти струны имеют дополнительную нагрузку в виде органа Корти, что имеет свой аналог в музыкальных инструментах, где стальные струны обматываются медной проволокой для понижения частоты их звучания.
Одна из таких струн рис.3, может содержать несколько коллагеновых волокон, которые вместе натянуты со средней силой Т, приложенной к сечению струны ![]() , где:
, где: ![]() – ширина струны;
– ширина струны; ![]() – толщина упругого слоя струны, зависящая от
– толщина упругого слоя струны, зависящая от![]() .
.
Эту силу можно определить выражением:
![]() ,
,
где: Е –модуль Юнга – коэффициент, характеризующий упругость материала струны, ![]() – относительное удлинение струны под действием силы Т.
– относительное удлинение струны под действием силы Т.
Рассмотрим теперь силы, действующие на элемент струны.
На поверхность элемента действует сила давления:
![]() ,
,
где: P– амплитуда давления звуковой волны; ![]() – круговая частота звука; f – частота звука; t – время; dx– ширина и dy– длина элемента струны.
– круговая частота звука; f – частота звука; t – время; dx– ширина и dy– длина элемента струны.
Сила инерции элемента, согласно второму закону Ньютона, равна:
![]() ,
,
где: ![]() - масса элемента;
- масса элемента; ![]() - его ускорение; ρ – средняя плотность (двухслойного) элемента струны;
- его ускорение; ρ – средняя плотность (двухслойного) элемента струны; ![]() – толщина струны.
– толщина струны.
При движении элемента он испытывает силу сопротивления жидкости окружающей среды, направленную противоположно его скорости:
![]() ,
,
где: α – коэффициент вязкости среды; ![]() - скорость элемента.
- скорость элемента.
Сила упругости струны, действующая на элемент и стремящаяся вернуть его в положение равновесия, зависит от искривления струны в месте расположения элемента и в линейном приближении равна:
![]()
Баланс всех сил действующих на элемент струны (уравнение его движения) определяется соотношением:
![]() (1)
(1)
Подставляя в (1) выражения для составляющих сил, получим дифференциальное уравнение вынужденных колебаний струны в вязкой среде [6]:
![]() (2)
(2)
Вводя обозначения:
![]() ;
; ![]() ;
; ![]() ,
,
запишем его в виде:
![]() (3)
(3)
Найдем решение этого уравнения - z(y,t) для установившихся стационарных колебаний, при которых вид решения не зависит от начальных условий (формы струны при t=0). Этот случай соответствует периодическому звуковому сигналу и является весьма характерным, хотя следует учитывать, что, например, при анализе речи, сигнал можно считать стационарным в течение всего 10 миллисекунд.
Граничные условия для концов струны определим равенством: ![]() , при
, при ![]() , что соответствует их жесткому закреплению.
, что соответствует их жесткому закреплению.
Кроме периодичности (во времени) звукового сигнала сделаем предположение о периодичности колебаний струны по пространственной координате у, считая струну бесконечной по длине. Такой чисто математический прием позволяет найти решение в классе периодических функций, а затем ограничиться реальным интервалом колебания (длиной) струны. Периодическую функцию можно в общем случае представить рядом Фурье. Учитывая приведенное выше граничное условие, получим следующее представление вида искомого решения:
![]() , (4)
, (4)
где коэффициенты разложения Фурье: ![]() , поскольку движение струны совершается с частотой вынуждающей силы. Амплитуду
, поскольку движение струны совершается с частотой вынуждающей силы. Амплитуду ![]() и нулевую фазу
и нулевую фазу ![]() каждой пространственной гармоники с номером n необходимо определить в процессе решения уравнения (3). Нулевая фаза колебаний гармоники определяется при сравнении с фазой звуковых колебаний в районе струны.
каждой пространственной гармоники с номером n необходимо определить в процессе решения уравнения (3). Нулевая фаза колебаний гармоники определяется при сравнении с фазой звуковых колебаний в районе струны.
По всей длине реальной (ограниченной) струны на все ее элементы действует в любой момент времени одинаковое давление звуковой волны, но для поддержания колебаний на условно бесконечной струне давление должно меняться вдоль нее на противофазное на каждом смежном по координате y участке длиной L. Последнее означает, что следует умножить коэффициент χ в уравнении (3) на функцию меандра M(y) с периодом 2L, изображенную на рис. 4.
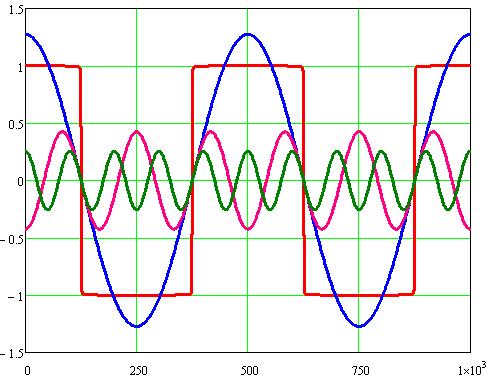
Ее можно разложить в ряд Фурье [7]:
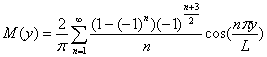 (5)
(5)
Это выражение показывает, что четные пространственные гармоники разложения равны нулю, а из нечетных гармоник каждая вторая берется со знаком минус. На рис. 4 приведены первая, третья и пятая гармоники разложения, причем третья гармоника инвертирована. Можно видеть, что для всех гармоник выполняются граничные условия, то есть их значения равны нулю, при ![]() .
.
Отсутствие четных пространственных гармоник в выражении для вынуждающей колебания струны силы давления, означает то, что, при случайном возникновении четной гармоники в колебаниях струны она быстро исчезнет благодаря некомпенсируемым силам трения. Следует отметить, что имеются опытные данные, указывающие на наличие особых поперечных противофазных колебаний основной мембраны улитки, вызванные движением внешних волосковых клеток органа Корти. Это обстоятельство следует учитывать при задании длины струны ![]() .
.
Запишем выражения для производных, входящих в (3), дифференцируя (4):
![]() ,
,
![]() ,
,
![]() .
.
Подставляя эти выражения в (3) с учетом (5), сокращая на величину ![]() и обозначая:
и обозначая: ![]() , получим для каждого из n выражение:
, получим для каждого из n выражение:
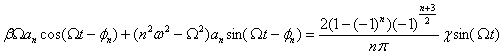 . (6)
. (6)
Составляющие этого выражения можно представить векторами (рис. 5), вращающимися против часовой стрелки с частотой Ω, с длинами:
![]() ,
, ![]() ,
, 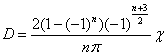 .
.
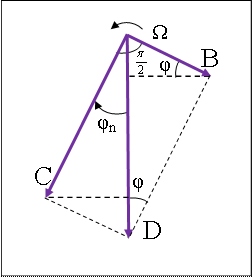
Рис.5. Соотношение векторов.
Очевидны следующие соотношения:
![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Из первого соотношения получим, при подстановке значений входящих в него величин, уравнение, решая которое найдем:
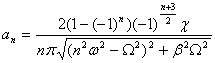 . (7)
. (7)
Из остальных соотношений, с учетом значения an, получим выражения для тригонометрических функций фазы φn:
![]() , (8)
, (8)
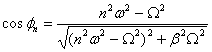 , (9)
, (9)
![]() . (10)
. (10)
Учитывая, что:
![]() ,
,
![]() ,
,
подставляя в (4) значения величин из (7), (8) и (9), получим решение уравнения (3):
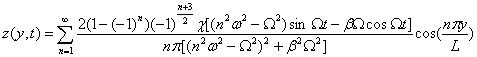 , (11)
, (11)
в котором величины:![]() ,
, ![]() ,
, ![]() ,
, ![]() являются в общем случае функциями координаты x и могут быть определены экспериментально.
являются в общем случае функциями координаты x и могут быть определены экспериментально.

