Кольца Френеля с синусоидальным профилем
- Информация о материале
- Категория: Испытательное изображение - кольца Френеля
- Опубликовано: 11.02.2019 18:23
- Автор: Павел Варгин
Введем прямоугольную систему координат с осью абсцисс – x и ординат – y. При этом изображение колец Френеля с синусоидальным профилем и со светлой центральной зоной, в соответствии с выражениями (5) и (6) определяется выражением:
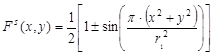 , (8)
, (8)
поскольку справедливо равенство: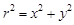 и где знак плюс перед функцией sin() соответствует позитивному, а минус – негативному изображению колец Френеля.
и где знак плюс перед функцией sin() соответствует позитивному, а минус – негативному изображению колец Френеля.
Представим цифровое изображение колец набором квадратных пикселей с центрами в узлах регулярной прямоугольной решетки, наложенной на континуальное изображение колец. Яркость пикселей определяется яркостью континуального изображения колец в узлах решетки. Такое изображение можно определить прямоугольной матрицей (массивом) – 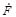 . Введем, как принято, нумерацию элементов цифрового изображения начиная с его верхнего левого угла. При этом, номер строки матрицы –
. Введем, как принято, нумерацию элементов цифрового изображения начиная с его верхнего левого угла. При этом, номер строки матрицы – 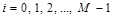 , номер столбца –
, номер столбца –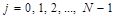 , а размер матрицы –
, а размер матрицы – 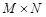 . Элемент изображения (матрицы, массива) обозначим символом –
. Элемент изображения (матрицы, массива) обозначим символом – 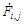 . Пусть начало координат x и y (центр колец Френеля) совпадает с центром пикселя
. Пусть начало координат x и y (центр колец Френеля) совпадает с центром пикселя 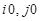 , тогда в выражении (8):
, тогда в выражении (8): 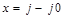 ,
,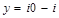 . Получим выражение для значений яркости элементов цифрового позитивного изображения колец с синусоидальным профилем с выборкой континуального значения в центре пикселя:
. Получим выражение для значений яркости элементов цифрового позитивного изображения колец с синусоидальным профилем с выборкой континуального значения в центре пикселя:
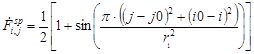 . (9)
. (9)
Аналогично, из (8), получим выражение для значений яркости элементов цифрового негативного изображения колец с синусоидальным профилем:
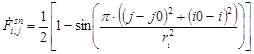 . (10)
. (10)
Выражения (9) и (10) позволяют синтезировать растровое (цифровое) изображение колец Френеля с синусоидальным профилем, при использовании, например, пакета Mathcad.
Проведем усреднение значений континуального образа колец по площади каждого из квадратных пикселей, на которые мы разбиваем этот образ. Такое усреднение можно представить интегрированием выражения (8) в пределах размеров пикселя – 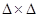 с последующей выборкой значений интеграла в центрах пикселей. Запишем выражение для интеграла:
с последующей выборкой значений интеграла в центрах пикселей. Запишем выражение для интеграла:
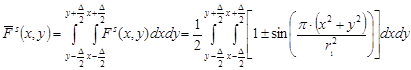 , (11)
, (11)
где знак плюс перед функцией sin() соответствует позитивному, а минус – негативному изображению колец Френеля.
Интеграл в правой части выражения (9) сводится к интегралам Френеля, которые не могут быть выражены в элементарных функциях. Вместе с тем, с хорошим приближением:
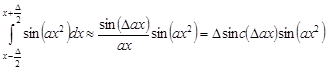 , (12)
, (12)
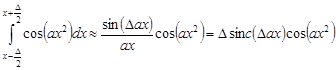 , (13)
, (13)
С учетом (12) и (13), в соответствии с (11), изображение колец Френеля с синусоидальным профилем, определяется выражением:
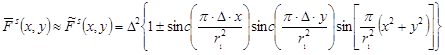 . (14)
. (14)
Предполагая, что расстояние между центрами пикселей, расположенными в узлах прямоугольной решетки, равно единице, а начало координат x и y (центр колец Френеля) совпадает с центром пикселя 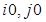 , получим выражение для значений яркости элементов (пикселей) цифрового изображения со светлым (знак плюс перед sinc функцией) или темным (знак минус перед sinc функцией) центром:
, получим выражение для значений яркости элементов (пикселей) цифрового изображения со светлым (знак плюс перед sinc функцией) или темным (знак минус перед sinc функцией) центром:
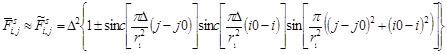 , (15)
, (15)
где: 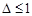 .
.
Это выражение позволяет синтезировать растровое изображение колец Френеля с синусоидальным профилем с усреднением значений континуального образа колец по площади каждого из квадратных пикселей, при использовании, например, пакета Mathcad и таким образом моделировать работу цифровой телевизионной камеры.

На рис. 3 слева приведено цифровое изображение колец Френеля синтезированное в соответствии с выражением (9) с учетом соотношения (3). Кроме основного центрального изображения колец это изображение содержит множество его прямых (позитивных) и инверсных (негативных) копий, так называемых посторонних узоров (ПУ). Наличие ПУ на изображении колец Френеля является характерным признаком цифрового изображения с регулярным растром. Используя выражения: (9), (10) или (15) можно изучать ПУ, воспроизводя графики профилей их изображений фиксируя какой-либо столбец или строку изображения.
На рис. 3 справа приведено цифровое изображение колец Френеля синтезированное в соответствии с выражением (15) с учетом соотношения (3). Кроме основного центрального изображения колец это изображение также содержит посторонние узоры, но они гораздо менее контрастные, чем основное центральное изображение колец и их контраст убывает к периферии рисунка, что обусловлено модулирующим действием sinc – функций выражения.
Изображения рис. 3 синтезированы при значениях: 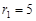 ,
,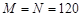 ,
,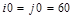 ,
,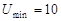 ,
,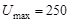 ,
,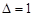 .
.

Поскольку выражение (15) является приближенным равенством, оно позволяет воспроизводить цифровое изображение колец Френеля с некоторой ошибкой. Ошибку синтеза изображения можно определить матрицей разностей элементов двух изображений, значение яркости которых вычисляются либо с использованием выражению (15), либо путем интегрирования выражения (11) с использованием численных методов. Разность элементов двух таких изображений определяется выражением:
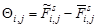 , (16)
, (16)
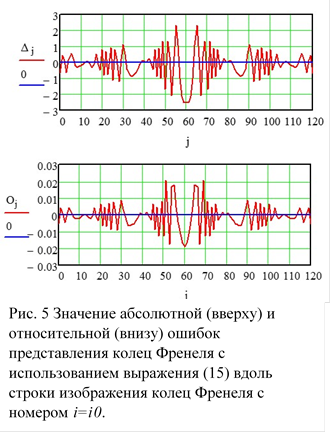
Матрицу таких элементов можно представить также в виде изображения. На рис. 4 отображены значения увеличенной в 50 раз ошибки представления элементов колец Френеля с помощью выражения (15). Эта ошибка уменьшается к краям изображения, где сравнима с величиной одного уровня квантования. Напомним, что с учетом контрастной чувствительности зрения, цифровое изображение обычно квантуется на 256 уровней яркости. На рисунке 5 вверху приведен график изменения абсолютного значения этой ошибки вдоль шестидесятой (центральной) строки изображения колец, рассчитанный по формуле:
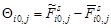 . (17)
. (17)
Можно видеть, что эта ошибка не превышает значения трех уровней квантования яркости.
На рисунке 5 снизу приведен график изменения относительного значения этой ошибки вдоль шестидесятой (центральной) строки изображения колец, рассчитанный по формуле:
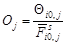 . (18)
. (18)
В данном случае относительная ошибка в основном меньше двух процентов, то есть практически зрительно не воспринимается, что оправдывает использование выражения (15).

