Разрешающая способность
- Информация о материале
- Категория: Чёткость и разрешающая способность цифровой телевизионной системы
- Опубликовано: 27.12.2018 17:45
- Автор: Павел Варгин
Продольная разрешающая способность аналоговой телевизионной системы может быть измерена визуально с помощью элементов телевизионной испытательной таблицы – групп вертикальных клинообразных чёрных и белых полосок по положению границы между различимыми и неразличимыми полосками группы относительно линейной шкалы. Этот метод измерений использован при разработке таблицы ИТ-72 (рис. 3), где указанные элементы размещены в центре и углах таблицы. Слева или справа от каждой группы размещена линейная шкала, деления которой обозначены точками и короткими горизонтальными штрихами, а штрихам сопоставлены колонки цифр от 3 до 6, которым соответствует разрешающая способность от 300 до 600 твл соответственно. При визуальном измерении разрешающей способности с использованием указанного метода пороговый контраст К задаётся зрительной системой наблюдателя элементов таблицы.
Важно отметить наличие групп клинообразных полосок не только в центре, но и в каждом из углов таблицы ИТ-72. Это позволяет определять качество оптики (объектива) телевизионной системы и, в частности, выявлять при испытаниях случаи перекоса установки оптической системы относительно фотодатчика изображения. Однако таблица ИТ-72 не подходит для определения визуальным методом разрешающей способности цифровых телевизионных систем из-за появления на изображениях групп ПУ (муаров). Если при измерении чёткости муары на зонных решетках необходимы, то при измерении разрешающей способности на группах клинообразных полосок они вредны, поскольку мешают определению границ различения полосок.
Цифровая телевизионная система отличается от аналоговой тем, что её изображение дискретизировано не только в вертикальном, но и в горизонтальном направлении и, кроме того, оно дискретизировано (квантовано) по яркости. Дискретизация, то есть замена непрерывного сигнала его выборками, в общем случае приводит к потере части информации, содержащейся в сигнале, что может приводить к искажениям сигнала, восстановленного с использованием выборок, по сравнению с исходным. Восстановление включает интерполяцию межвыборочных значений сигнала. Обычно, для воспроизведения изображения используют ступенчатую интерполяцию нулевого порядка, когда каждой выборке соответствует одна светящаяся площадка (ступенька, пиксель) экрана. С развитием технологии создания телевизионных экранов и появлением стандартов разложения высокой и сверхвысокой чёткости (см. табл.) возникает проблема их совместимости со стандартами меньшей чёткости, при решении которой следует использовать интерполяцию более высоких порядков. Например, двумерную линейную или с использованием двумерных квадратичных или кубических сплайнов. В данном случае интерполирующие функции вычисляются лишь в точках, соответствующих расположению пикселей экрана повышенной чёткости, а далее следует опять ступенчатая интерполяция. Фактически, в этом случае производится передискретизация изображения с целью повышения чёткости.
Рассмотрим особенности процесса воспроизведения чёрно-белых решёток цифровой телевизионной системой с помощью его математического моделирования. Решётку можно характеризовать числом штрихов на высоту видимого растра. При этом ширина горизонтального штриха, спроецированного на фотодатчик, выраженная в пикселях, определяется выражением:
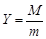 , (5)
, (5)
где: М – число строк фотодатчика (чёткость), m – число штрихов.
Профиль решетки вдоль выбранного направления х, можно описать некоторой периодической функцией E(x, X) с периодом X.
Любую функцию f(x), заданную на отрезке X, можно сделать периодической с периодом X, подстановкой в неё вместо аргумента x, функции «повторитель» («репитер»):
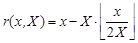 , (6)
, (6)
где: ë×û – обозначение Айверсона функции – «пол» – округление вниз. Задание периодических функций с помощью повторителя обеспечивает быстрое их вычисление, поскольку операция округления быстрая.
Профиль прямоугольной решетки с шириной штриха Y можно задать с помощью функции «меандр» с периодом 2Y, используя повторитель. При этом функция «меандр» для вертикального направления y определяется выражением:
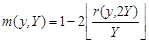 , (7)
, (7)
График этой функции приведён на рис. 4 пунктиром. С использованием меандра профиль прямоугольной (бинарной) решетки:
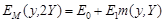 , (8)
, (8)
где: E0 – среднее значение освещённости фотодатчика, E1 – амплитуда освещённости.
Сигнал элемента фотодатчика – сенселя (sensor element) с номером i определяется выражением:
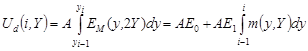 , (9)
, (9)
где: yi–1 = i – 1 и yi = i – координаты верхней и нижней границ пикселя, A – чувствительность фотодатчика (В/лк).
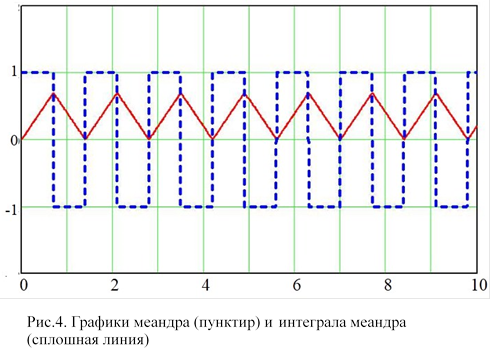
Неопределённый интеграл от функции «меандр» представляет собой пилообразную функцию с периодом 2Y, показанную на рис. 4 сплошной линией, с использованием повторителя определяется выражением:
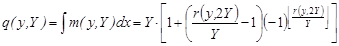 . (10)
. (10)
С учётом (9) и (10), а также возможного сдвига вниз положения решетки относительно сенселей Dy, получим аналитическое выражение для дискретного сигнала сенселя с номером i:
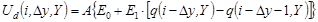 , (11)
, (11)
Интерполятор нулевого порядка определяется выражением:
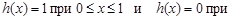
других значениях x, (12)
а ступенчатая интерполяция видеосигнала фотодатчика:
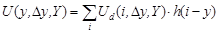 . (13)
. (13)
На рис. 5 приведены графики видеосигналов фотодатчика, рассчитанные в соответствии с (13) при помощи Mathcad для E0 = 0,5, E1 = 0,4, Y = 1, с различными сдвигами решетки Dy относительно сенселей.
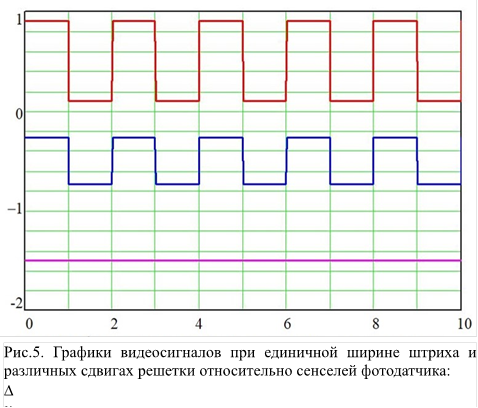
Dy = 0 (вверху), Dy = 0,2 (в середине), Dy = 0,5 (внизу)
Первый график (вверху) соответствует освещению нечётных сенселей и затенению чётных, что обеспечивает максимальную амплитуду видеосигнала. Второй (в середине) соответствует большему освещению нечётных и меньшему чётных сенселей, что приводит к уменьшению потенциального рельефа фотодатчика. Третий график (внизу) соответствует одинаковой освещённости сенселей при сдвиге изображения штрихов на половину сенселя, что приводит к полному исчезновению потенциального рельефа и, соответственно, телевизионного изображения решетки чёрно-белых штрихов.
Приведенный вариант расчёта иллюстрирует большое значение относительного сдвига оптического изображения штриха и положения сенселя фотодатчика. Поскольку, при ширине изображения штриха не равной единице сдвиг изменяется вдоль растра, видеосигнал и, соответственно, изображение решетки цифровой телевизионной системы меняется самым причудливым образом. Например, на рис. 6 приведены графики видеосигналов фотодатчика при Y= 0,9 и сдвигах: Dy = 0 и Dy = 0,5. Можно видеть, что в данном случае потенциальный рельеф не исчезает, при начальном сдвиге на половину сенселя, но изменяется, по сравнению с нулевым сдвигом. Можно также заметить, что в обоих случаях профиль видеосигнала имеет собственный период, равный девяти сенселям (пикселям).
При ширине штриха, выраженной в виде приведенной дроби Y = a/b, собственный период независимо от сдвига равен:
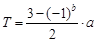 , (14)
, (14)
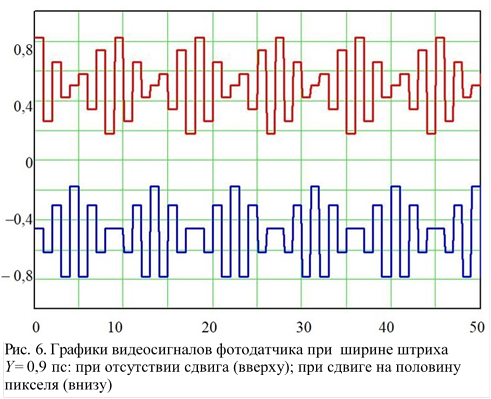
В приведённом в начале статьи определении разрешающей способности телевизионной системы содержится условие задания порогового контраста. Контраст объекта периодической структуры (контрастность Майкельсона) определяется выражением;
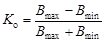 , (15)
, (15)
где Bmax и Bmin – максимальная и минимальная его яркости.Другое название этой величины – модуляция.
Контраст телевизионного изображения решетки штрихов, как и картина потенциального рельефа, также зависит и от ширины штриха Y и от сдвига Dy решетки относительно сенселей. Максимальный реализуемый контраст (МРК) изображения прямоугольной решетки идеальной телевизионной системы достигается совмещением границы смежных сенселей и границы двух смежных штрихов. Для прямоугольной решетки это локальный контраст.
Будем считать телевизионную систему идеальной, если она не имеет искажений, кроме связанных с переходом к дискретному изображению. Обозначим МРК идеальной телевизионной системы, воспроизводящей прямоугольную в профиле решетку штрихов, символом KMR и, анализируя значение этой величины на различных интервалах толщины штриха – Y, найдем, что:
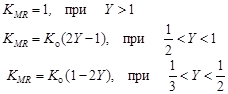 , (16)
, (16)
где: Kо – контраст решетки чёрных и белых штрихов, согласно выражению (15).
Любую телевизионную систему можно оценивать функцией передачи максимального реализуемого контраста (ФП МРК):
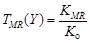 , (17)
, (17)
которая в соответствии с выражениями (16), зависит только от величины Y.
Удобно выражать эту функцию в виде зависимости от величины обратной толщине штриха Y, которую можно назвать частотой штрихов. Для горизонтально расположенных штрихов обозначим эту частоту буквой v, для вертикально расположенных – u. При этом для идеальной телевизионной системы в соответствии с выражениями (16) и (17):
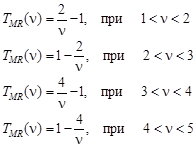 . (18)
. (18)
Как можно видеть, здесь удобство заключается в том, что интервалы частоты штрихов одинаковы по величине, то есть шкала частот линейна.
ФП МРК идеальной дискретной телевизионной системы при наблюдении решетки прямоугольного профиля в общем случае определяется как:
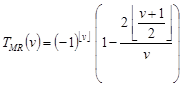 (19)
(19)
На рис. 7 приведён график ФП МРК, полученный с использованием выражения (19) (сплошная линия). Функция TMR(ν), характеризующая идеальную телевизионную систему с дискретизацией изображения и не зависящая от сдвига изображения относительно сенселей фотодатчика телевизионной камеры, может служить эталоном для сравнения с функцией передачи максимального реализуемого контраста реальной телевизионной системы Tmr(ν), полученной в результате испытаний телевизионной системы.
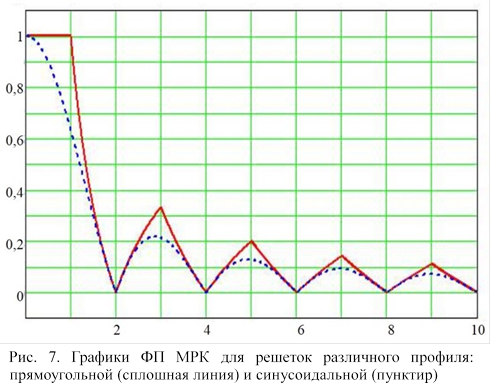
На рис. 7 также приведён график ФП МРК (пунктир) идеальной телевизионной системы с использованием синусоидально-модулированной решетки, примеры изображения которой показаны на рис. 8. Такие решетки могут использоваться для определения характеристик телевизионных систем наряду с описанными выше решетками с профилем в виде меандра.
Использование подобных решёток осложняется более жесткими требованиями к технологии воспроизведения их профиля на испытательных таблицах. Для синусоидальной решетки профиль освещённости матрицы фотодатчика в вертикальном направлении определяется выражением:
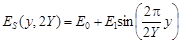 , (20)
, (20)
где: E0 и E1 – постоянная составляющая и амплитуда решетки.
Это выражение можно сравнить с (8): и то, и другое можно преобразовать в функции от пространственной частоты. При этом выражению (20) соответствует:
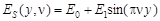 , (21)
, (21)
где v – пространственная частота, т. е. количество полупериодов синусоиды, приходящихся на сенсель фотодатчика. МРК телевизионного изображения такой решетки не является локальным, то есть не может быть определен контрастом соседних сенселей при любом сдвиге решетки относительно сенселей фотодатчика.

Для определения МРК синусоидальной решетки необходимо получить (реализовать) симметричное расположение сенселя как относительно положительной полуволны синусоиды, так и относительно отрицательной. Если такие расположения получены, то максимальный реализуемый сигнал сенселя определяется выражением:
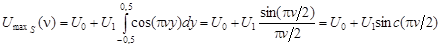 , (22)
, (22)
а минимальный сигнал:
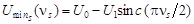 , (23)
, (23)
где: U0 = AE0, U1 = AE1.
Максимальный реализуемый контраст (МРК) синусоидальной решетки:
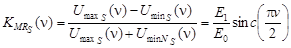 . (24)
. (24)
Поскольку контраст синусоидальной решетки Kоs = E1/E0, то ФП МРК синусоидальной решетки определяется выражением, соответствующим графику, изображенному на рис. 7 пунктиром:
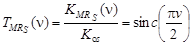 . (25)
. (25)
Оба графика ФП МРК на рис. 7 для идеальной телевизионной системы при наблюдении прямоугольной и синусоидальной решеток достигают нулевых значений только в точках с чётными целыми значениями ν и отличны от нуля во всех других точках. ФП МРК реальной телевизионной системы отлична от нуля лишь на конечном интервале пространственных частот. Высокие пространственные частоты обычно подавляются оптической системой телевизионной камеры или специальными электронными фильтрами.
Дискретный сигнал сенселя с номером i при синусоидально модулированной решетке определяется выражением:
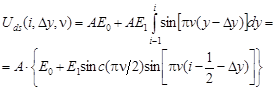 . (26)
. (26)

