Гексагональная решетка
- Информация о материале
- Категория: Контурное кодирование изображений
- Опубликовано: 13.05.2022 21:45
- Автор: Павел Варгин
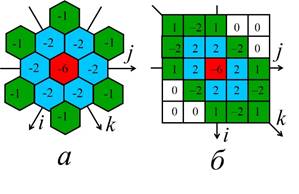

Гексагональные решетки для представления изображений обладают рядом преимуществ по сравнению с квадратными решетками пикселей. В частности, обладая более равномерным соединением пикселей в решетке, они обеспечивают лучшее угловое разрешение благодаря наличию большего числа ближайших соседей. Они лучше (более гладко) представляют контуры объектов [6, 7]. Ввиду высокой плотности упаковки гексагональные решетки широко распространены в зрительных системах различных организмов.
Выделение контуров
На рис. 6 а) приведена маска из шестиугольных элементов – «снежинка», полученная как результат последовательного применения прямой и обратной конечных разностей в трех различных направлениях осей: i, j, и k, расположенных под углом 600 друг к другу. Такая маска является дискретным аналогом трехмерной частной производной второго порядка. На рис. 6 б) приведена прямоугольная карта «снежинки», где ее оси сдвинуты до углов 450. Разумеется, при приведенном плоском картировании неизбежны визуальные искажения, но карта позволяет проводить с ней вычисления и отображать результаты на обычном прямоугольном растре.
Другим способом отображения маски рис. 6 а) является ее представление в трехмерном пространстве в виде своеобразного «кубика Рубика», который состоит из 27 меньших кубиков – вокселей. Воксели имеют различные веса: угловые – «1», средние ребер – «-2», средние граней – «4», а центральный – «-6». При этом оси: i, j, и k, проходящие через центр «кубика Рубика» и центры боковых граней, взаимно перпендикулярны.
Кроме выражений: (1), (2) для оси – i и (4), (5) для оси – j, приведем выражения для отображения оси – k на карту обратной конечной разности:
![]() (16)
(16)
и прямой конечное разности:
![]()
(17)
Подставляя в последнее выражение значения всех предыдущих получим аналитическое выражение для двумерной карты гексагональной маски дискретного аналога трехмерной производной второго порядка (рис. 6 б), при Y = s, при этом начало отсчета выберем в правом нижнем углу карты:
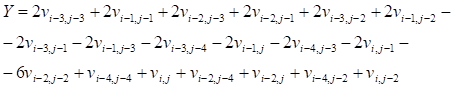
. (18)
На рис. 7 приведены изображения: а) тестовое – v, б) масштабированное контурное – Y, в) контрастированное контурное с обрезкой модуля значений пикселей больше 120 – Y и масштабированное и г) контурное в псевдоцветах с красными положительными и

синими отрицательными значениями контуров – Y. Все изображения на рис. 7 получены аналогично изображениям на рис.2, но с картой гексагональной маски – «снежинки».
Сравнивая контурные (кодированные) изображения рисунков 2, 3, 4 и 7 можно видеть, что все они различны несмотря на то, что соответствуют одному исходному изображению. Их различие объясняется различием масок, с которыми производится свертка исходного изображения. Часто для оценки эффективность кодирования изображений используют оценки их информационного сжатия. В частности, коэффициент сжатия, представляющий собой отношение размеров выходного и входного файлов кодера или обратная ему величина фактор сжатия. Эти оценки достаточно трудно сделать, поскольку размер выходного файла зависит от энтропии исходного изображения, которую достаточно сложно вычислить, ввиду ее зависимости от вероятностной модели изображения, которую еще необходимо построить. С другой стороны, легко оценить интегральную мощность сигналов пикселей исходного и кодированного изображений и далее оценить выигрыш в мощности при кодировании взяв их отношение. Последняя оценка хотя и не связана прямо со скоростью передачи информации по каналу связи позволяет оценить снижение энергетических затрат при такой передаче. В соответствии с вышесказанным выигрыш в мощности определяется выражением:
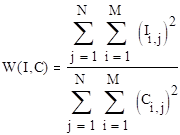
, (19)
где I и C – матрицы исходного и кодированного (контурного) изображения; Ii, j и Ci, j – элементы исходного и кодированного изображений; M и N – число строк и столбцов изображений, соответственно. Подставляя в выражение (19) матрицы исходного изображения – v и масок E, K, L и Y, получим соответствующие выигрыши в мощности:
![]()
![]()
![]()
![]()

Согласно этим значениям, наибольший выигрыш достигается при использовании маски – E. Что касается маски Y, то расчет для нее производился по карте маски, а не напрямую и поэтому не подлежит сравнению с остальными масками.
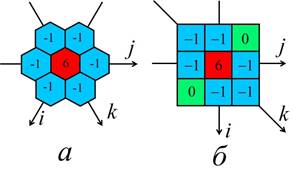
Рассмотрим еще одну гексагональную маску. На рис. 8 а) приведен ее вид, а на рис. 8 б) ее прямоугольная карта. Эта маска напоминает графическое изображение рецептивного поля ганглиозной клетки сетчатки глаза и поэтому обозначим ее буквой – R. Алгоритм свертки исходного изображения – v с картой этой маски представляется выражением, которое схоже с выражением (8) за исключением двух угловых элементов, которые в карте равны нулю и веса центрального элемента:
![]()
(20)
|
|


Выигрыш в мощности для исходного изображения – v и маски R согласно выражению (19) равен: W(v, R) = 3,685, что больше, чем W(v, Y). Заметим, что выигрыш в мощности для биологических систем весьма важен, поскольку дает им преимущество в выживании.
На рис. 9 приведены изображения: а) тестовое – v, б) масштабированное контурное – R, в) контрастированное контурное с обрезкой модуля значений пикселей больше 120 – R и масштабированное и г) контурное в псевдоцветах с красными положительными и синими отрицательными значениями контуров – R. Все изображения на рис. 7 получены аналогично изображениям на рис.2, но с картой гексагональной маски – «рецептивное поле» – R.
Восстановление изображения
Алгоритм восстановления (декодирования) из контурного – Y изображения исходного изображения v = Vy, можно получить используя уравнение (18). Из которого следует, что:
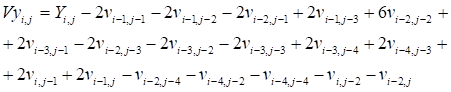
(21)
При этом известны граничные значения:
Vy1,j = Y1,j = v1,j, Vy2,j = Y2,j = v2,j, Vy3,j = Y3,j = v3,j, Vy4,j = Y4,j = v4,j
Vyi,1 = Yi,1 = vi,1, Vyi,2 = Yi,2 = vi,2, Vyi,3 = Yi,3 = vi,3, Vyi,4 = Yi,4 = vi,4
и расчет ведется для элементов исходного изображения в интервале номеров:
5 ≤ i ≤ M и 5 ≤ j ≤ N.
Таким образом, порядок восстановления из Y – контурного изображения исходного отличается от предыдущих случаев более широкой границей, что определяется размером карты маски этого изображения.
Алгоритм восстановления (декодирования) из контурного – R изображения исходного изображения v = Vr, можно получить используя уравнение (20). Из которого следует, что:
![]() (22)
(22)
При этом известны граничные значения:
Vr1,j = R1,j = v1,j, Vr2,j = R2,j = v2,j,
Vri,1 = Ri,1 = vi,1, Vri,2 = Ri,2 = vi,2
и расчет ведется для элементов исходного изображения в интервале номеров:
3 ≤ i ≤ M и 3 ≤ j ≤ N.
На рис. 10 показаны некоторые возможные варианты порядка восстановления небольшого исходного изображения при M = 10 и N = 9.
В варианте а) восстановление начинается с элемента, обозначенного номером «1» белым цветом, и продолжается вдоль третьей строки изображения в порядке следования обозначенных номеров элементов. Эта строка для наглядности выделена тонально (красным цветом). Следующая (четвертая) строка восстановления также выделенная тонально (зеленым цветом) начинается с номера «1», продолжается номером «2» и далее до номера «7». Последующие строки восстанавливаются в аналогичном приведенному порядке. При этом восстанавливающая маска движется вдоль строки касаясь своим нижним элементом очередного элемента изображения. Гексагональная восстанавливающая маска для первого восстановленного элемента изображения выделена тонально и обозначена буквой Ц на своем центре. Таким образом производится последовательная (поэлементная) обработка изображения. Верхняя скошенная граница данного варианта изображения имеет толщину в два элемента, боковые в один элемент, а нижняя граница отсутствует.
В варианте б) восстановление также начинается с элемента, обозначенного номером «1», затем «2», затем одновременно восстанавливаются сразу два элемента с номером «3», затем одновременно два элемента с номером «4», затем три элемента с номером «5» и далее последующие горизонтальные, тонально выделенные, строки изображения. Таким
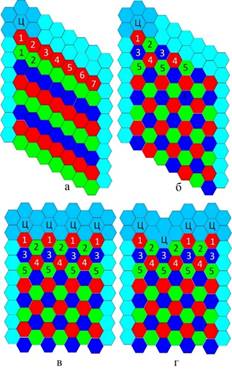

образом производится параллельная (построчная) обработка изображения, при движении сверху вниз «волны вычислений», фронт которой совпадает с очередной строкой изображения.
В варианте в) верхняя граница изображения уже не скошенная, а прямая. Обработка изображения ведется параллельно, построчно, при движении волны вычислений сверху вниз.
В варианте г) верхняя граница изображения не прямая, а со сдвигом вниз одного из ее столбцов. Обработка изображения, как и в двух предыдущих вариантах ведется параллельно, построчно, при движении волны вычислений сверху вниз. Этот вариант показывает, что граница изображения не обязательно должна быть прямолинейной.
Во всех вариантах важно, чтобы каждый из восстанавливаемых элементов изображения в момент восстановления входил элементом в какую-либо маску восстановления, так чтобы значения всех остальных накрываемых маской элементов изображения на момент восстановления были известны.
Отметим выигрыш по времени при параллельной обработке контурного изображения на гексагональной решетке при восстановлении, что особенно важно, когда изображения должны быстро изменяться. Например, для варианта в) число тактов времени при параллельном восстановлении равно числу восстановленных строк M = 15, а при последовательном, при числе элементов в строке N = 4, требуется M х N = 60 тактов, т. е. в четыре раза больше, что снижает частоту кадров в четыре раза. При M ≈ N выигрыш во времени составляет величину пропорциональную квадратному корню из числа элементов изображения без границ.
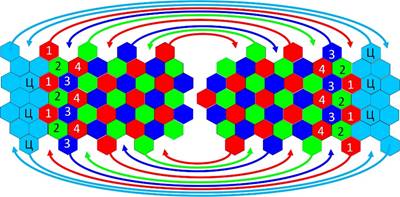

Интересным примером организации решетки изображения представляется зрительная кора головного мозга человека, на которую отображается сетчатка глаза. Она разделена на две половины в левой и правой затылочных областях мозга. Каждая из двух половин зрительной коры, при ее расположении на плоскости, представляет собой слегка усеченный на одном конце эллипс [8] на который проецируется одна из двух половин сетчатки, левого или правого поля зрения. На рис.11 приведена модель такой коры. Усеченные «эллипсы» справа и слева рисунка «склеены» (в топологическом смысле) по направлениям, указанным стрелками так, что элементы в начале стрелок входят в места, указанные их остриями без перекрытия элементов. Аналогом стрелок в мозге являются нервные волокна соединяющие половины зрительной коры. После склейки образуется поверхность, напоминающая кожуру огурца с обрезанным концом. На эту поверхность топографически проецируется контурное изображение объектов, спроецированных на сетчатку хрусталиком глаза. Преобразование исходного оптического изображения на сетчатке в дискретное контурное осуществляется благодаря центрально-симметричной on-off организации рецептивных полей ганглиозных (передающих) нейронов сетчатки [4]. В описанной ситуации мы можем предположить, что контурное изображение может быть восстановлено в исходное, методом, рассмотренном в настоящей статье на ряде примеров. При этом граница изображения представляет собой замкнутое кольцо, соответствующее срезу кожуры «огурца», а кольцеобразный фронт «волны вычислений» распространяется от границы в направлении самой удаленной от границы точки поверхности коры. Заметим, что граница соответствует периферии поля зрения, которая, согласно исследованиям А. Л. Ярбуса [9], освещается равномерно – усредненно. При таком освещении достаточно передавать на границу зрительной коры только данные о средней освещенности, увеличивая таким образом выигрыш в мощности при контурном кодировании. Наличие волновых процессов в зрительной коре обнаружено И. А. Шевелевым [10].


